Racine carrée d'un nombre complexe
Tout nombre complexe non nul admet exactement deux racines carrées, qui sont opposées! On a deux méthodes pour résoudre z
2=w :
- Écrire w=a+ib, z=x+iy, et procéder par identification des coefficients. Utiliser le module permet d'apporter une équation supplémentaire qui simplifie beaucoup!
- Utiliser la forme trigonométrique de w, si elle est facilement accessible. On raisonne alors comme pour les racines n-ièmes (cf infra).
Exemple :On souhaite résoudre z
2=2+i. On pose z=x+iy. Nous avons :

où les constantes valent plus ou moins 1. La condition 2xy=1 nous permet d'affirmer que les solutions sont :
 Equation du second degré
Equation du second degré
Soit (E) l'équation az
2+bz+c=0, d'inconnue z, où a,b,c sont des complexes, et a est non nul. Le discriminant de cette équation est

:
- Si le discriminant est nul, alors l'équation (E) admet une racine double : z=-b/2a.
- Si le discriminant est non nul soit
 l'une des racines carrées (complexe) de ce discriminant. Alors (E) admet deux racines complexes :
l'une des racines carrées (complexe) de ce discriminant. Alors (E) admet deux racines complexes :

Remarque : Ainsi, tout polynôme du second degré à coefficients complexes admet une racine dans l'ensemble des nombres complexes. Plus généralement, le théorème de d'Alembert-Gauss dit que tout polynôme non constant à coefficients complexes admet une racine dans
C.
Racines n-ièmes d'un nombre complexe non nul
Si w est un nombre complexe non nul, et n un entier naturel non nul, on appelle racine n-ième de w tout nombre complexe tel que z
n=w.
Tout nombre complexe non nul admet exactement n racines n-ièmes.

La méthode de recherche est la suivante :
 O
On appelle racine n-ième de l'unité les racines n-ièmes dans
C du nombre complexe 1. Elles sont données par :

L'ensemble des racines n-ièmes de l'unité est un groupe cyclique d'ordre n du groupe (
C*,×). La racine w
k engendre ce groupe si et seulement si les entiers k et n sont premiers entre eux.



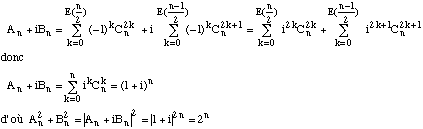



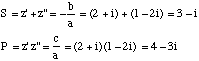














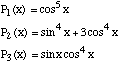





 . Le module vérifie les propriétés suivantes :
. Le module vérifie les propriétés suivantes :
 |z|+|z'| (inégalité triangulaire).
|z|+|z'| (inégalité triangulaire).
 un réel tel que :
un réel tel que :











 :
:
 l'une des racines carrées (complexe) de ce discriminant. Alors (E) admet deux racines complexes :
l'une des racines carrées (complexe) de ce discriminant. Alors (E) admet deux racines complexes :










 est le symétrique de M par rapport à l'axe (Ox).
est le symétrique de M par rapport à l'axe (Ox).
 est réel.
est réel.

